OrbMol: Extending Orb to Molecular Systems
Articles
Kareem Abdelmaqsoud was the primary author of this work, which he conducted as part of an internship with Orbital Materials
We’re excited to release OrbMol, our most recent addition to the Orb family of models. Where Orb is designed for inorganic crystals, OrbMol is built for molecules. Built on the Orb-v3 architecture, OrbMol leverages the Open Molecules 2025 (OMol25) dataset—over 100M high-accuracy DFT calculations (ωB97M-V/def2-TZVPD) [1]. As a result, OrbMol accurately models metal complexes, biomolecules, and electrolytes. OrbMol can also condition on total charge and spin multiplicity, a critical feature for the design of many novel materials & molecules.
Our Orb models are known for excellent inference speed while maintaining state of the art accuracy. OrbMol is no different. It beats prior state of the art models on many benchmarks, while being at least 2x faster and more memory efficient. We also see excellent agreement in molecular dynamics with many experimentally observed results.
As always, Orb is released under the permissive apache2 license. We’re excited to see what bringing quantum accuracy at high speeds brings to the world of molecular design - biology, organic electronics, organic chemistry.
Evaluation
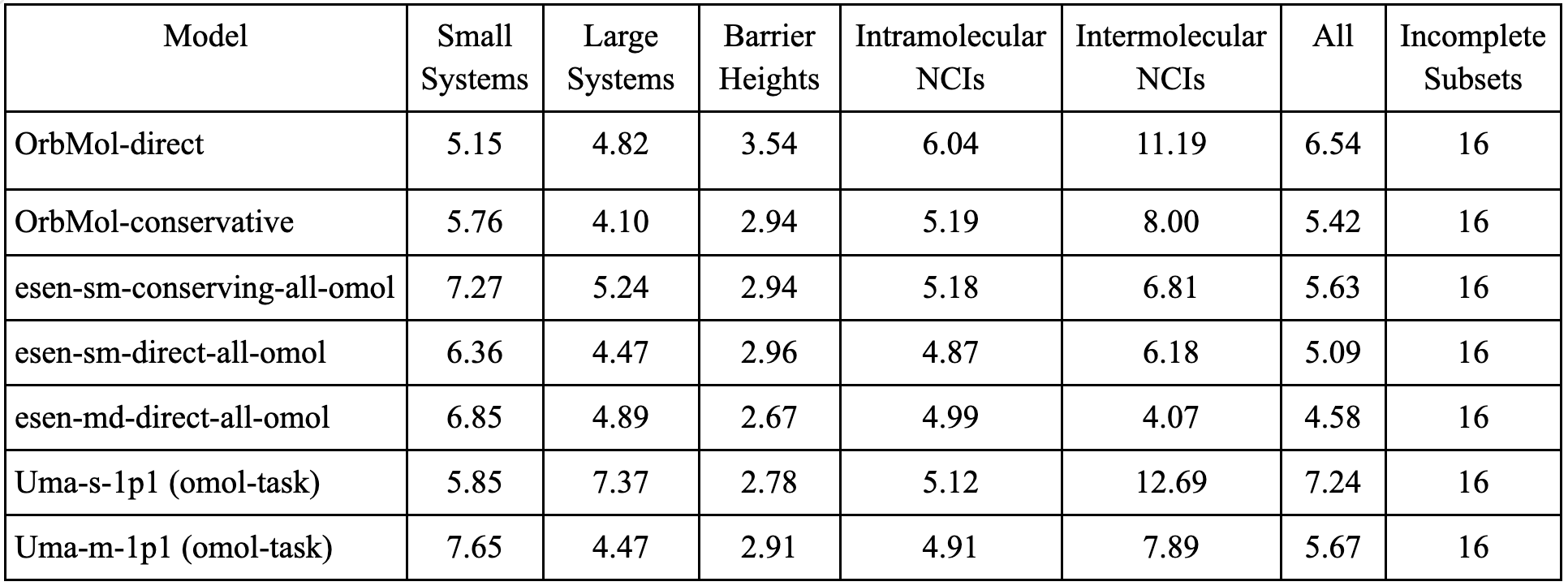
The GMTKN55 benchmark is a comprehensive test suite for evaluating computational chemistry methods on main-group thermochemistry, kinetics, and noncovalent interactions [2]. We focus on the results of conservative models below, but include the results of direct models in the appendix. Figure 1 shows that the conservative OrbMol model achieves lower or comparable errors to the eSEN and UMA models, and slightly lower overall on the full benchmark. This highlights the consistently high performance of OrbMol on these diverse and essential chemical problems.
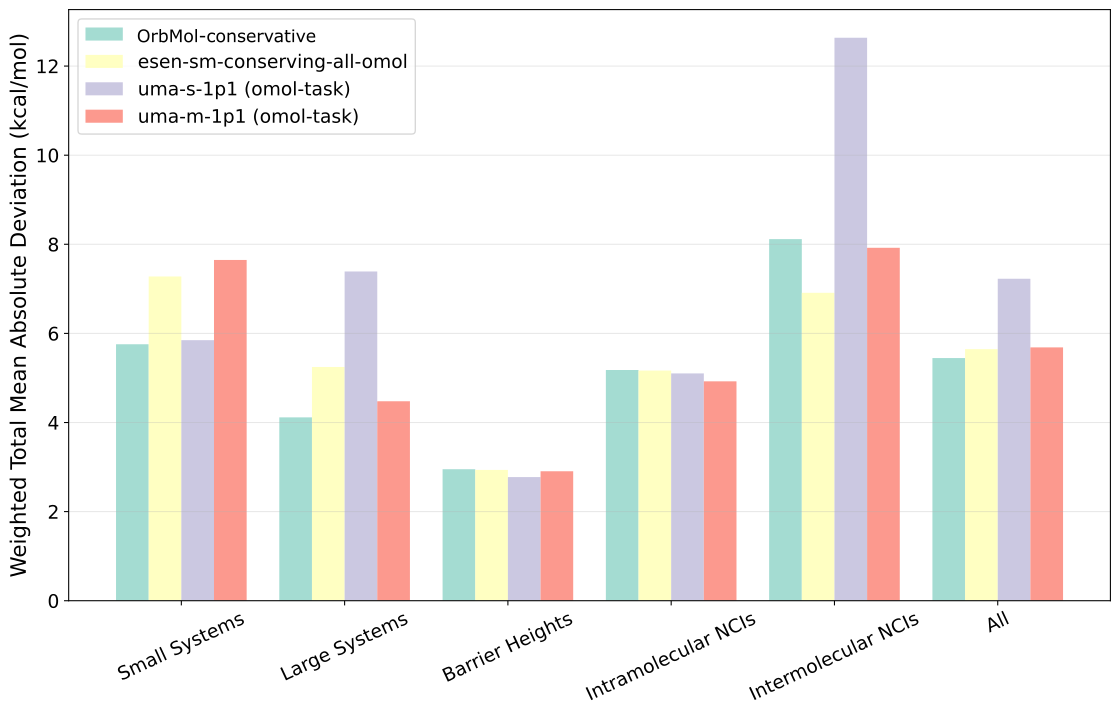
Figure 1: GMTKN55 benchmark. The category-level metrics are computed using the weighted total mean absolute deviation based on assigned difficulty WTMAD-2 weights.
The PLA15 benchmark measures protein–ligand interaction energies for 15 complexes containing 600–2000 atoms [3]. It enables fair evaluation of computational methods on systems too large for direct quantum-chemical calculations, bridging the gap between small-molecule benchmarks and realistic drug design targets. Figure 2 shows that OrbMol has a percentage error distribution that is less wide than eSEN and UMA and does not have large outliers similar to the small eSEN or small UMA models. This benchmark shows that low-cost methods such as machine learning potentials can maintain near-DFT accuracy.
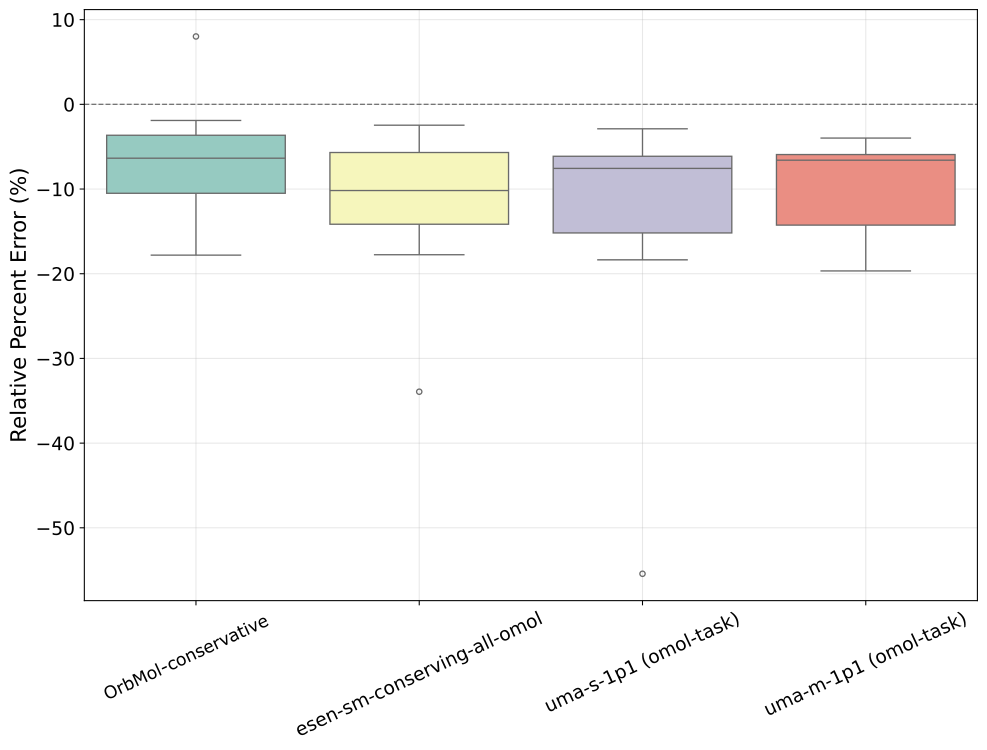
Figure 2: The PLA15 benchmark. Box plot showing the distribution of the percentage errors in predicting the interaction energies of 15 protein-ligand complexes.
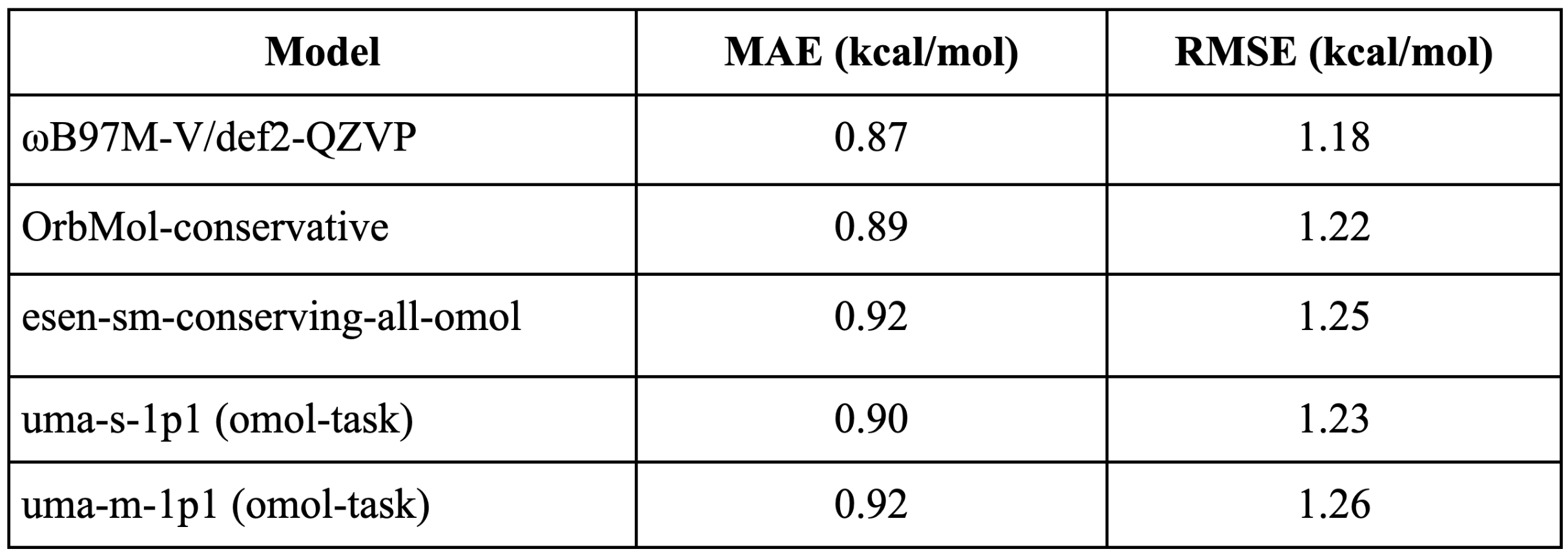
The Wiggle 150 benchmark evaluates the accuracy of predicting and ranking of highly-strained conformers. It focuses on non-equilibrium structures unlike most benchmarks [4]. It is composed of 150 highly strained conformations of adenosine, benzylpenicillin, and efavirenz. OrbMol shows error on par with the expensive ωB97M-V/def2-QZVP DFT method. The errors are lower than 1 kcal/mol which is considered chemical accuracy. This demonstrates that OrbMol is capable of reliably modeling high-strain molecular conformations at a fraction of the cost of traditional quantum-chemical methods.
Table 1: Shows the mean absolute errors (MAE) and Root Mean Square Error (RMSE) in kcal/mol in calculating energies of the conformers in the wiggle 150 benchmark. OrbMol shows performance similar to the DFT as well as eSEN and UMA models.
Molecular Dynamic Simulations
The model can be used for stable molecular dynamics simulation and gives a highly accurate description of the molecular structure of pure water and water around a sodium ion as shown in Figure 3.
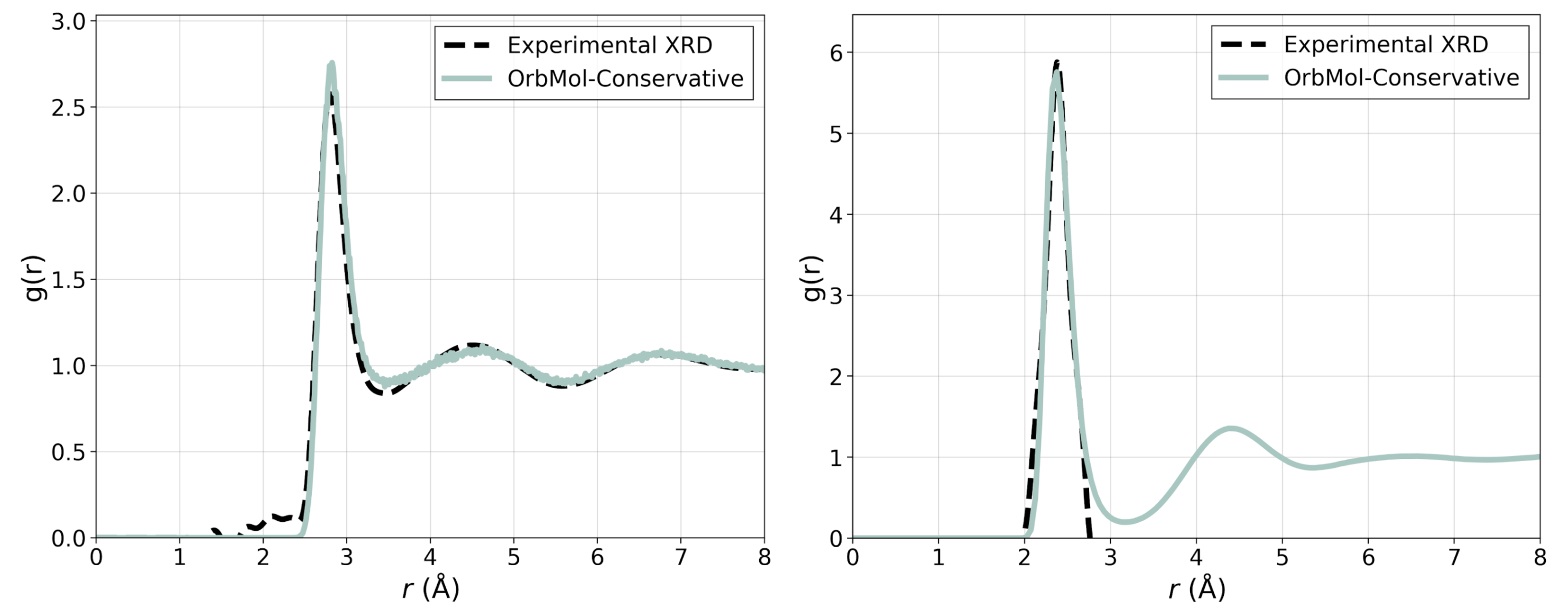
Figure 3: Oxygen-oxygen and sodium oxygen radial distribution function with OrbMol-Conservative in comparison with experimental X-ray diffraction (XRD) data taken from Ref. [5] and [6].
To test OrbMol's ability to simulate more complex systems we simulated a fully solvated carbonic anhydrase II enzyme [7] (see Figure 4) composed of over 20,000 atoms including a coordinated zinc metal ion for over 230 ps with no constraints. The resulting structure remains stable compared to the original PDB structure with a very low RMSD of 0.6 Å. (See Figure 4) For context, simulations using classical forcefields and the Orb-v3-Direct-Inf-mpa model both result in RMSDs that increases to over 2 Å over similar time scales [8].
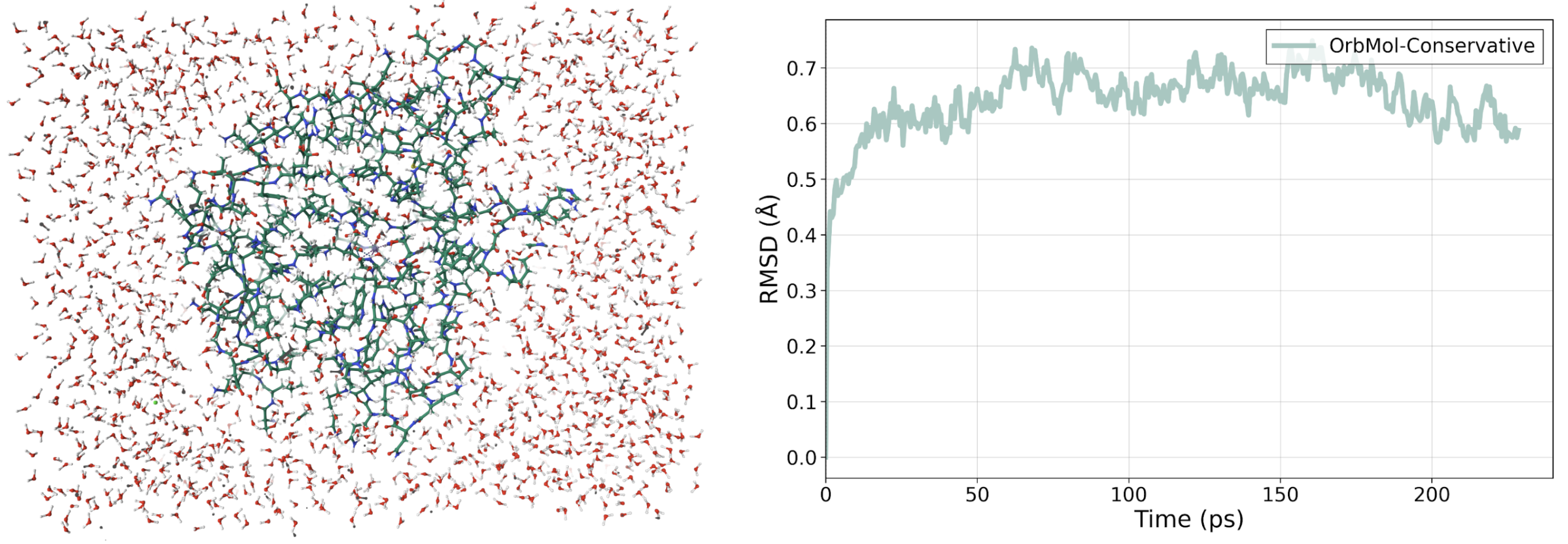
Figure 4: A fully solvated carbonic anhydrase II enzyme [7] that can be stably simulated with OrbMol-conservative on a single H200 GPU. Comparison of the simulated structure and the original PDB structure of carbonic anhydrase II [7] and the RMSD of backbone carbon atoms as a function of time showing very low RMSD.
Additionally, during the simulation a CO2 randomly placed within the active site of the enzyme quickly displaced two water molecules and moved into the known binding site adjacent to the zinc, surrounded by hydrophobic residues as shown in Figure 5. This phenomena was not observed with Orb-v3-Direct-Inf-mpa. This demonstrates the ability of this model to capture weak physisorption/dispersion interactions.

Figure 5: Active site of the carbonic anhydrase enzyme with CO2 bound to the experimentally observed site and the distance between the CO2 and zinc over time reproducing the experimentally observed distance [9].
Simulation details
Molecular dynamics simulations were performed using the Atomic Simulation Environment (ASE) package [10] with Langevin dynamics [11] at room temperature (300 K) with a friction coefficient of 0.01 and NVT ensemble. Images were made with Mol* [12].
References
1. Levine, D. S.; Shuaibi, M.; Spotte-Smith, E. W. C.; Taylor, M. G.; Hasyim, M. R.; Michel, K.; Batatia, I.; Csányi, G.; Dzamba, M.; Eastman, P.; Frey, N. C.; Fu, X.; Gharakhanyan, V.; Krishnapriyan, A. S.; Rackers, J. A.; Raja, S.; Rizvi, A.; Rosen, A. S.; Ulissi, Z.; Vargas, S.; Zitnick, C. L.; Blau, S. M.; Wood, B. M. The Open Molecules 2025 (OMOL25) dataset, evaluations, and models. arXiv.org. https://arxiv.org/abs/2505.08762.
2. Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2017, 19 (48), 32184–32215. https://doi.org/10.1039/C7CP04913G.
3. Kříž, K.; Řezáč, J. Benchmarking of Semiempirical Quantum-Mechanical Methods on Systems Relevant to Computer-Aided Drug Design. J. Chem. Inf. Model. 2020, 60 (3), 1453–1460. https://doi.org/10.1021/acs.jcim.9b01171.
4. Brew, R. R.; Nelson, I. A.; Binayeva, M.; Nayak, A. S.; Simmons, W. J.; Gair, J. J.; Wagen, C. C. Wiggle150: Benchmarking Density Functionals and Neural Network Potentials on Highly Strained Conformers. J. Chem. Theory Comput. 2025, 21 (8), 3922–3929. https://doi.org/10.1021/acs.jctc.5c00015.
5. Skinner, L. B.; Huang, C.; Schlesinger, D.; Pettersson, L. G. M.; Nilsson, A.; Benmore, C. J. Benchmark Oxygen-Oxygen Pair-Distribution Function of Ambient Water from X-Ray Diffraction Measurements with a Wide Q-Range. J. Chem. Phys. 2013, 138 (7), 074506. https://doi.org/10.1063/1.4790861.
6. Galib, M.; Baer, M. D.; Skinner, L. B.; Mundy, C. J.; Huthwelker, T.; Schenter, G. K.; Benmore, C. J.; Govind, N.; Fulton, J. L. Revisiting the Hydration Structure of Aqueous Na+. J. Chem. Phys. 2017, 146 (8), 084504. https://doi.org/10.1063/1.4975608.
7. Avvaru, B. S.; Kim, C. U.; Sippel, K. H.; Gruner, S. M.; Agbandje-McKenna, M.; Silverman, D. N.; McKenna, R. A Short, Strong Hydrogen Bond in the Active Site of Human Carbonic Anhydrase II. Biochemistry 2010, 49 (2), 249–251. https://doi.org/10.1021/bi902007b.
8. Mapar, M.; Taghdir, M.; Ranjbar, B. Comparative Study of Stability and Activity of Wild-Type and Mutant Human Carbonic Anhydrase II Enzymes Using Molecular Dynamics and Docking Simulations. Biochem. Biophys. Res. Commun.2024, 734, 150720. https://doi.org/10.1016/j.bbrc.2024.150720.
9. Domsic, J. F.; Avvaru, B. S.; Kim, C. U.; Gruner, S. M.; Agbandje-McKenna, M.; Silverman, D. N.; McKenna, R. Entrapment of Carbon Dioxide in the Active Site of Carbonic Anhydrase II. J. Biol. Chem. 2008, 283 (45), 30766–30771. https://doi.org/10.1074/jbc.M805353200.
10. Larsen, A. H.; Mortensen, J. J.; Blomqvist, J.; Castelli, I. E.; Christensen, R.; Dułak, M.; Friis, J.; Groves, M. N.; Hammer, B.; Hargus, C.; Hermes, E. D.; Jennings, P. C.; Jensen, P. B.; Krogstrup, J.; Jørgensen, M.; Kuisma, M.; Lastra, J. M. G.; Lathiotakis, N. N.; Olsen, T.; Petzold, V.; Romero, A. H.; Schiøtz, J.; Strange, M.; Thygesen, K. S.; Vegge, T.; Vilhelmsen, L.; Walter, M.; Zeng, Z.; Jacobsen, K. W. The Atomic Simulation Environment—a Python Library for Working with Atoms. J. Phys. Condens. Matter 2017, 29 (27), 273002. https://doi.org/10.1088/1361-648X/aa680e.
11. Vanden-Eijnden, E.; Ciccotti, G. Second-Order Integrators for Langevin Equations. Chem. Phys. Lett. 2006, 429 (1-3), 310–316. https://doi.org/10.1016/j.cplett.2006.07.034.
12. Sehnal, D.; Bittrich, S.; Deshpande, M.; Svobodová, R.; Berka, K.; Bazgier, V.; Velankar, S.; Burley, S. K.; Koča, J.; Rose, A. S. Mol* Viewer: Modern Web App for 3D Visualization and Analysis of Large Biomolecular Structures. Nucleic Acids Res. 2021, 49 (W1), W431–W437. https://doi.org/10.1093/nar/gkab314.
13. Karton, A.; Chan, B. PAH335 – A Diverse Database of Highly Accurate CCSD(T) Isomerization Energies of 335 Polycyclic Aromatic Hydrocarbons. Chem. Phys. Lett. 2023, 824, 140544. https://doi.org/10.1016/j.cplett.2023.140544.
14. Rhodes, B.; Vandenhaute, S.; Šimkus, V.; Gin, J.; Godwin, J.; Duignan, T.; Neumann, M. Orb-v3: atomistic simulation at scale. arXiv.org. https://arxiv.org/abs/2504.06231.
Appendix:
GMTKN55 benchmark full results
We also exclude subsets that include single-atom systems to enable fair comparison with the eSEN and UMA models which return the DFT calculated energies for single atom systems. These are the 16 incomplete subsets shown in the table.
Table 2: Weighted mean absolute deviations (using WTMAD-2 scheme weights) for the different material classes across all the orb, eSEN and UMA models. The eSEN direct models show lower errors, but this advantage does not hold across the other benchmarks.
PLA15 benchmark full results
Table 3: Shows correlation and mean absolute percentage error (MAPE) between the model predicted energies and ground truth values.

Wiggle 150 benchmark full results
Table 4: Shows the mean absolute error (MAE) and root mean absolute error (RMSE) of the relative energies (conformer energy - min(conformer energies)) for each of the 3 molecules in the Wiggle 150 benchmark.

PAH335 benchmark full results:
The PAH335 benchmark is a diverse database of highly accurate CCSD(T) isomerization energies of 335 polycyclic aromatic hydrocarbons [13].
Table 5: Shows the median absolute deviation (MAD), Mean Squared Deviation (MSD) and Root Mean Square Deviation (RMSD) and the correlations for the PAH335 benchmark.

Speed and memory benchmarking
Speed and maximum GPU memory allocated on an NVIDIA H100 for the computation of energies and forces of FCC carbon crystal structures with different numbers of atoms. Periodic boundary condition (PBC) was enabled because the system tested is a crystalline material. Torch compilation was enabled for all orb models. Torch compilation was also enabled for eSEN and UMA models except for the cases where the compilation caused the model to run out of memory.
The direct and conservative orb models show higher inference speed than the corresponding direct and conservative eSEN and UMA models. eSEN and UMA models show better memory scaling to larger system sizes. Unlike the direct orb model which uses 120 maximum neighbors, the direct eSEN models use only 30 neighbors which could lead to discontinuity in the potential energy surface[14].
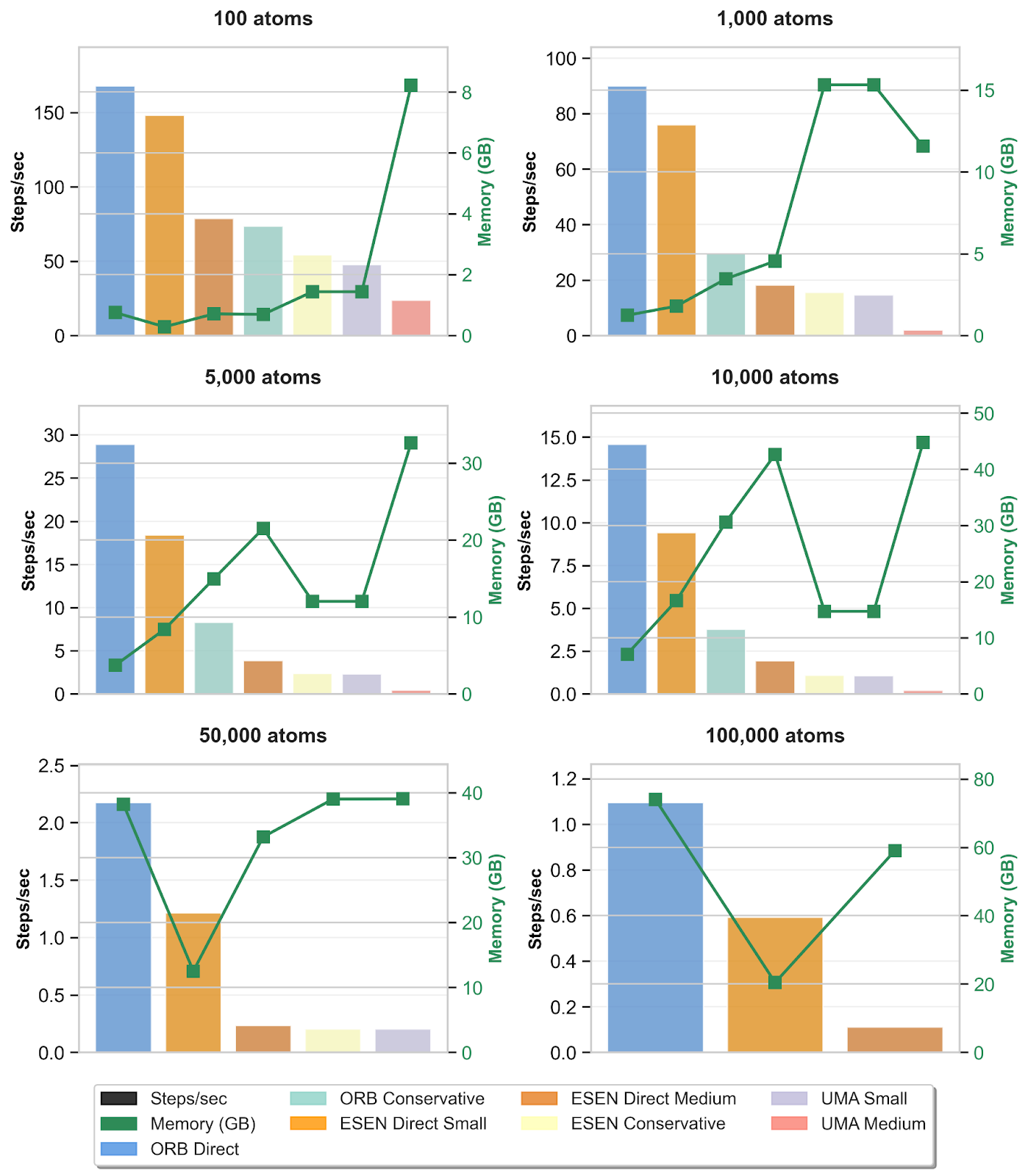
Figure 6: Speed and maximum memory usage benchmarking of orb, eSEN and UMA models on NVIDIA H100 GPU for the computation of energies and forces of FCC carbon crystal structures with different numbers of atoms. Models that are missing from the subplots of the higher number of atoms ran out of memory.
Energy and force errors break down by material class
Table 6: The breakdown of the energy and force MAEs across the different material classes in the OMol25 validation set. We should emphasize that all of these errors are below chemical accuracy (e.g. force errors below ~1 kcal/mol/Å = ~40 meV/Å). The medium eSEN has the lowest energy and force errors, but is ~15x slower than the direct OrbMol model.